Albert Einstein discoveries #2
Einstein Field Equation
The Einstein field equations (EFE) or Einstein's equations are a set of 10 equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy. First published by Einstein in 1915 as a tensor equation, the EFE equate local spacetime curvature (expressed by the Einstein tensor) with the local energy and momentum within that spacetime (expressed by the stress–energy tensor). The Einstein field equations (EFE) may be written in the form:
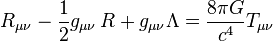
where is the Ricci curvature tensor,
is the Ricci curvature tensor, 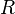 the scalar curvature,
the scalar curvature, 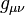 the metric tensor,
the metric tensor, 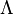 is the cosmological constant,
is the cosmological constant, 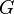 is Newton's gravitational constant,
is Newton's gravitational constant,  the speed of light in vacuum, and
the speed of light in vacuum, and  the stress–energy tensor.
the stress–energy tensor.
Bose–Einstein correlations
Classical unified field theories
EPR paradox
The Einstein field equations (EFE) or Einstein's equations are a set of 10 equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy. First published by Einstein in 1915 as a tensor equation, the EFE equate local spacetime curvature (expressed by the Einstein tensor) with the local energy and momentum within that spacetime (expressed by the stress–energy tensor). The Einstein field equations (EFE) may be written in the form:
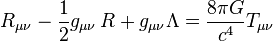
where
 is the Ricci curvature tensor,
is the Ricci curvature tensor, 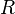 the scalar curvature,
the scalar curvature, 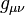 the metric tensor,
the metric tensor, 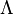 is the cosmological constant,
is the cosmological constant, 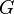 is Newton's gravitational constant,
is Newton's gravitational constant,  the speed of light in vacuum, and
the speed of light in vacuum, and  the stress–energy tensor.
the stress–energy tensor.
Bose-Einstein statistics
In quantum statistics, Bose–Einstein statistics (or more colloquially B–E statistics) is one of two possible ways in which a collection of non-interacting indistinguishable particles may occupy a set of available discrete energy states, at thermodynamic equilibrium. The aggregation of particles in the same state, which is a characteristic of particles obeying Bose–Einstein statistics, accounts for the cohesive streaming of laser light and the frictionless creeping of superfluid helium. The theory of this behaviour was developed (1924–25) by Satyendra Nath Bose, who recognized that a collection of identical and indistinguishable particles can be distributed in this way. The idea was later adopted and extended by Albert Einstein in collaboration with Satyendra Nath Bose.
The Bose–Einstein statistics apply only to those particles not limited to single occupancy of the same state—that is, particles that do not obey the Pauli exclusion principle restrictions. Such particles have integer values of spin and are named bosons, after the statistics that correctly describe their behaviour. There must also be no significant interaction between the particles.
Bose–Einstein condensate (BEC)
A Bose–Einstein condensate (BEC) is a state of matter of a dilute gas of bosons cooled to temperatures very close to absolute zero (that is, very near 0 K or −273.15 °C). Under such conditions, a large fraction of the bosons occupy the lowest quantum state, at which point quantum effects become apparent on a macroscopic scale. These effects are called macroscopic quantum phenomena.
Although later experiments have revealed complex interactions, this state of matter was first predicted, generally, in 1924–25 by Satyendra Nath Bose and Albert Einstein.
In physics, Bose–Einstein correlations are correlations between identical bosons. They have important applications in astronomy, optics, particle and nuclear physics. The interference between two (or more) waves establishes a correlation between these waves. In particle physics, in particular, where to each particle there is associated a wave, we encounter thus interference and correlations between two (or more) particles, described mathematically by second or higher order correlation functions. These correlations have quite specific properties for identical particles. We then distinguish Bose–Einstein correlations for bosons and Fermi–Dirac correlations for fermions. While in Fermi–Dirac second order correlations the particles are antibunched, in Bose–Einstein correlations (BEC) they are bunched. Another distinction between Bose–Einstein and Fermi–Dirac correlation is that only BEC can present quantum coherence.
Since the 19th century, some physicists have attempted to develop a single theoretical framework that can account for the fundamental forces of nature – a unified field theory. Classical unified field theories are attempts to create a unified field theory based on classical physics. In particular, unification of gravitation and electromagnetism was actively pursued by several physicists and mathematicians in the years between World War I and World War II. This work spurred the purely mathematical development of differential geometry. Albert Einstein is the best known of the many physicists who attempted to develop a classical unified field theory.
The EPR paradox is an early and influential critique leveled against the Copenhagen interpretation of quantum mechanics. Albert Einstein and his colleagues Boris Podolsky and Nathan Rosen (known collectively as EPR) designed a thought experiment which revealed that the accepted formulation of quantum mechanics had a consequence which had not previously been noticed, but which looked unreasonable at the time. The scenario described involved the phenomenon that is now known as quantum entanglement.
According to quantum mechanics, under some conditions, a pair of quantum systems may be described by a single wave function, which encodes the probabilities of the outcomes of experiments that may be performed on the two systems, whether jointly or individually. At the time the EPR article discussed below was written, it was known from experiments that the outcome of an experiment sometimes cannot be uniquely predicted. An example of such indeterminacy can be seen when a beam of light is incident on a half-silvered mirror. One half of the beam will reflect, the other will pass. If the intensity of the beam is reduced until only one photon is in transit at any time, whether that photon will reflect or transmit cannot be predicted quantum mechanically.
CREDIT: wikipedia.org

Comments
Post a Comment